
CPA
Foundation Leval
Quantitative Analysis September Pilot 2015
Suggested solutions

Revision Kit

| ➧ | Quantitative Analysis -September-2015-Pilot-Paper |
| ➧ | Quantitative Analysis-November-2015-Past-Paper |
| ➧ | Quantitative Analysis-May-2016-Past-paper |
| ➧ | Quantitative Analysis-November-2016-Past-Paper |
| ➧ | Quantitative Analysis-December-2017-Past-paper |
| ➧ | Quantitative Analysis-May-2017-Past-paper |
| ➧ | Quantitative Analysis-November-2018-Past-paper |
| ➧ | Quantitative Analysis-May-2018-Past-paper |
| ➧ | Quantitative Analysis-May-2019-Past-paper |
| ➧ | Quantitative Analysis-November-2019-Past-paper |
| ➧ | Quantitative Analysis-November-2020-Past-paper |
| ➧ | Quantitative Analysis-December-2021-Past-paper |
| ➧ | Quantitative Analysis-April-2021-Past-paper |
| ➧ | Quantitative Analysis-August-2021-Past-paper |


QUESTION 1(a)
QUESTION 1(b)
| Number of clients |
Market Share |
Flow of clients | Number of clients |
Market Share |
||||||
| Gains from | Losses to | |||||||||
X Y Z |
31.12.2013 408 832 1,062 |
0.177 0.361 0.461 |
X - 30 18 |
Y 24 - 14 |
Z 40 10 - |
X - 24 40 |
Y 30 - 10 |
Z 18 14 - |
31.12.2014 424 834 1044 |
0.184 0.362 0.454 |
|
To
From
|
X | Y | Z |
| X | - | 30/408 = 0.074 | 18/408 = 0.044 |
| Y | 24/832 = 0.029 | - | 14/832 = 0.017 |
| Z | 40/1062 = 0.038 | 10/1062 = 0.009 | - |
| Firm | No.of clients | Market share |
| X Y Z |
437 836 1029 |
0.190 0.363 0.447 |
| Total | 2302 | 1.000 |
QUESTION 1(c)
QUESTION 2(a)
QUESTION 2(b)
| Marketer Hours worked (x) Earnings (Sh. “000”) (y) |
1 20 5.5 |
2 30 7.4 |
3 48 11.0 |
4 39 9.3 |
5 28 7.2 |
6 14 4.3 |
7 60 13.5 |
8 50 12.0 |
9 62 14.0 |
10 43 10.0 |
| X | Y"000" | XY | X2 |
| 20 | 5.5 | 110 | 400 |
| 30 | 7.4 | 222 | 900 |
| 48 | 11 | 528 | 2,304 |
| 39 | 9.9 | 362.7 | 1,521 |
| 28 | 7.2 | 201.6 | 784 |
| 14 | 4.3 | 90.2 | 196 |
| 60 | 13.5 | 810 | 3,600 |
| 50 | 12 | 600 | 2,500 |
| 62 | 14 | 868 | 3844 |
| 43 | 10 | 430 | 1849 |
| 394 | 94.2 | 4,193.5 | 17,898 |
| X | Y | Rx | Ry | d = Rx - Ry | d2 |
| 20 30 48 39 28 14 60 50 62 43 |
5.5 7.4 11 9.3 7.2 4.3 13.5 12 14 10 |
9 7 4 6 8 10 2 3 1 5 |
9 7 4 6 8 10 2 3 1 5 |
0 0 0 0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 0 0 0 |
QUESTION 3(a)
Production Light Dark |
Selling price (Sh.) per litre 13.00 16.00 |
Unit variable cost (Sh.) per litre 9.00 10.00 |
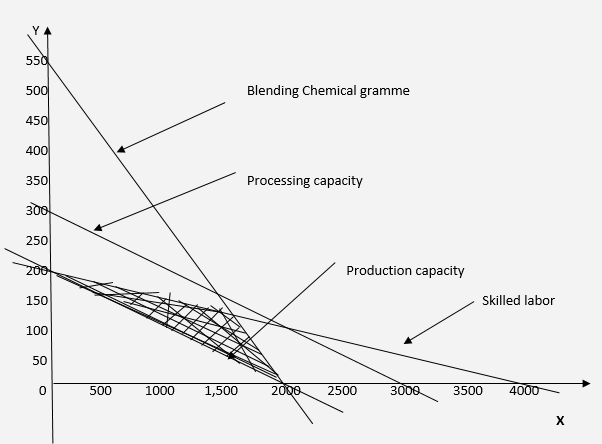
QUESTION 3(b)
| Market survey | Actual state of nature | ||
| Result G P |
H 0.7 0.3 |
M 0.6 0.4 |
L 0.2 0.8 |
| State of demand | |||
| High(H) | Moderate(M) | Low(L) | |
| Decision alternative Open new plant Do nothing |
0.3 6,000,000 0 |
0.3 1,500,000 0 |
0.4 -2,500,000 0 |
| State of nature | |||||
| High(H) | Moderate(M) | Low(L) | Total | ||
| 0.30 | 0.30 | 0.40 | |||
| Market Survay Report |
G (0.7 | 0.6 | 0.2) P (0.3 | 0.4 | 0.8) |
(0.7 x 0.3) = 0.21 (0.3 x 0.3) = 0.9 |
(0.6 x 0.3) = 0.18 (0.4 x 0.3) = 0.12 |
(0.2 x 0.4) = 0.08 (0.8 x 0.4) = 0.32 |
0.47 0.53 |
| Total | 0.3 | 0.3 | 0.4 | 1.0 | |

QUESTION 4(a)
Non-zero sum game: In a non-zero sum game, the total amount of wealth or utility can change, and the participants can collectively win or lose. Cooperation and coordination can lead to outcomes where all participants gain.
Pure strategy game: In a pure strategy game, players choose a specific action or strategy with certainty. There is no randomness in the decision-making process.
Mixed strategy game: In a mixed strategy game, players choose their strategies based on a probability distribution. The decision-making involves randomness, and players may use a mix of different strategies with certain probabilities.
QUESTION 4(b)
| Activity A B C D E F G H I J K L M |
Predecessory activity - - A A A A,B C C,D E G,H H H,I H,I,F |
Time(Days) 10 12 10 9 13 17 12 14 13 12 10 14 13 |

QUESTION 5(a)
QUESTION 5(b)
| Sales (Sh. "000,000") Quarter |
||||
| Year 2012 2013 2014 |
1 2.2 2.9 3.2 |
2 5 5.2 5.8 |
3 7.9 8.2 9.1 |
4 3.2 3.8 4.1 |
Year |
Quarter(Q) |
Sales(Y) |
4QMA |
4CMAT |
Seasonal fluctuation (Sales(Y) - 4CMAT) |
2012 2013 2014 |
1 2 3 4 1 2 3 4 1 2 3 4 |
2.2 5 → 7.9 → 3.2 → 2.9 → 5.2 → 8.2 → 3.8 → 3.2 → 5.8 → 9.1 4.1 |
4.575 → 4.75 → 4.8 → 4.875 → 5.025 → 5.10 → 5.25 → 5.475 → 5.55 |
4.663 4.775 4.838 4.950 5.063 5.175 5.363 5.513 |
3.237 -1.575 -1.938 0.25 3.137 -1.375 -2.163 0.287 |
| Year | Quarter 1 | Quarter 2 | Quarter 3 | Quarter 4 | |
| 2012 2013 2014 |
- -1.9375 -2.1625 |
- 0.25 0.2875 |
3.2375 3.1375 - |
-1.575 -1.375 - |
|
| Total index Average index Adjusted index Round off |
-4.1 -2.05 -2.038125 -2.0 |
0.5375 0.26875 0.2859375 0.3 |
6.375 3.1875 3.2046875 3.2 |
-2.95 -1.475 -1.4578125 -1.5 |
-0.1375 -0.06875 0 0 |
| Year | Quarter | Sales | Seasonal index | Deseasonalized data
(Sales - index) |
| 2012 | 1 2 3 4 |
2.2 5 7.9 3.2 |
-2.0 0.3 3.2 -1.5 |
4.2 4.7 4.7 4.7 |
| 2013 | 1 2 3 4 |
2.9 5.2 8.2 3.8 |
-2.0 0.3 3.2 -1.5 |
4.9 4.9 5 5.3 |
| 2014 | 1 2 3 4 |
3.2 5.8 9.1 4.1 |
-2.0 0.3 3.2 -1.5 |
5.2 5.5 5.9 5.6 |
QUESTION 5(c)
| ➦ | Economics-September-2015-Pilot-Paper |
| ➦ | Economics-November-2015-Past-Paper |
| ➦ | Economics-May-2016-Past-paper |
| ➦ | Economics-November-2016-Past-Paper |
| ➦ | Economics-November-2017-Past-paper |
| ➦ | Economics-May-2017-Past-paper |
| ➦ | Economics-November-2018-Past-paper |
| ➦ | Economics-May-2018-Past-paper |
| ➦ | Economics-May-2019-Past-paper |
| ➦ | Economics-November-2019-Past-paper |
| ➦ | Economics-November-2020-Past-paper |
| ➦ | Economics-December-2021-Past-paper |
| ➦ | Economics-April-2021-Past-paper |
| ➦ | Economics-August-2021-Past-paper |

| ➧ | Introduction to Law and Governance-September-2015-Pilot-Paper |
| ➧ | Introduction to Law and Governance-November-2015-Past-Paper |
| ➧ | Introduction to Law and Governance-May-2016-Past-paper |
| ➧ | Introduction to Law and Governance-November-2016-Past-Paper |
| ➧ | Introduction to Law and Governance-May-2017-Past-paper |
| ➧ | Introduction to Law and Governance-November-2017-Past-Paper |
| ➧ | Introduction to Law and Governance-November-2018-Past-paper |
| ➧ | Introduction to Law and Governance-May-2018-Past-paper |
| ➧ | Introduction to Law and Governance-May-2019-Past-paper |
| ➧ | Introduction to Law and Governance-November-2019-Past-paper |
| ➧ | Introduction to Law and Governance-November-2020-Past-paper |
| ➧ | Introduction to Law and Governance-December-2021-Past-paper |
| ➧ | Introduction to Law and Governance-April-2021-Past-paper |
| ➧ | Introduction to Law and Governance-August-2021-Past-paper |
| ➧ | Financial Accounting -September-2015-Pilot-Paper |
| ➧ | Financial Accounting -November-2015-Past-Paper |
| ➧ | Financial Accounting -May-2016-Past-paper |
| ➧ | Financial Accounting-November-2016-Past-Paper |
| ➧ | Financial Accounting-November-2017-Past-paper |
| ➧ | Financial Accounting-May-2017-Past-paper |
| ➧ | Financial Accounting-November-2018-Past-paper |
| ➧ | Financial Accounting-May-2018-Past-paper |
| ➧ | Financial Accounting-May-2019-Past-paper |
| ➧ | Financial Accounting-November-2019-Past-paper |
| ➧ | Financial Accounting-November-2020-Past-paper |
| ➧ | Financial Accounting-December-2021-Past-paper |
| ➧ | Financial Accounting-April-2021-Past-paper |
| ➧ | Financial Accounting-August-2021-Past-paper |
CPA past papers with answers